Tree

完全二叉树

只有最下面的两层结点度小于2，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树，不一定有排序；

满二叉树

除了叶结点外每一个结点都有左右子叶且叶结点都处在最底层的二叉树。

平衡二叉树（AVL）

平衡二叉树（Balanced Binary Tree）是二叉查找树（也称为排序二叉树，左小于右）的一个进化体，也是第一个引入平衡概念的二叉树。1962年，G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树，所以它又叫AVL树。平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

可能有这种说法

• 一种二叉搜索树
  1.所有非叶子结点至多拥有两个儿子（Left和Right）；
  2.左边小于右边，大局观也是如此；
• 特点
  1.当B树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么B树
  的搜索性能逼近二分查找（从线性到log2N），有利于增删改查；
  2.同时它比连续内存空间的二分查找的优点是，这些操作不需要移动大段的内存数据，甚至通常是常数开销；
• 使用
  尽量将元素构建为左边平衡的结构:
  
  

Treap树堆

作用：Treap的特点是实现简单，且能基本实现随机平衡的结构,避免变为链式结构。

一棵treap是一棵修改了结点顺序的二叉查找树。通常树内的每个结点x都有一个关键字值key[x]，另外，还要为结点分配priority[x]，treap的结点排列成让关键字遵循二叉查找树性质，并且优先级遵循最小堆顺序性质：

1. 如果v是u的左孩子，则key[v] < key[u].
2. 如果v是u的右孩子，则key[v] > key[u].
3. 如果v是u的孩子，则priority[u] > priority[v].

• treap插入操作：
  1.按照二叉树的插入方法，将结点插入到树中
  2.根据堆的性质(我们这里为最小堆)和优先级的大小调整结点位置，旋转不破坏排序树的特征。

• treap删除操作：
  1.找到相应的结点
  2.若该结点为叶子结点，则直接删除；
  若该结点为只包含一个叶子结点的结点，则将其叶子结点赋值给它；
  若该结点为其他情况下的节点，则进行相应的旋转，直到该结点为上述情况之一，然后进行删除。

具体例子见：http://blog.csdn.net/yang_yulei/article/details/46005845

B-树

• M叉搜索树

1. 定义任意非叶子结点最多只有M个儿子；且M>2；
2. 根结点的儿子数为[2, M]；
3. 除根结点以外的非叶子结点的儿子数为[M/2, M]；
4. 每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）
5. 非叶子结点的关键字个数=指向儿子的指针个数-1；
6. 非叶子结点的关键字：K1, K2, …, K[M-1]；且K[i] < K[i+1]；
7. 非叶子结点的指针：P1, P2, …, P[M]；其中P1指向关键字小于K1的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；
8. 所有叶子结点位于同一层；

• 特点

1. 关键字集合分布在整颗树中；
2. 任何一个关键字出现且只出现在一个结点中；
3. 搜索有可能在非叶子结点结束；
4. 其搜索性能等价于在关键字全集内做一次二分查找；
5. 自动层次控制；
6. 根节点使用关键字个数：最多M-1,最少M/2-1，向上取整

• 使用
  M=3:
  
  
  
  
  例子：http://blog.csdn.net/u013400245/article/details/52824744

B+树

• 与B-树的差异

1. 有n棵子树的结点中含有n个关键字，每个关键字不保存数据，只用来索引，所有数据都保存在叶子节点。
2. 所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
3. 所有的非终端结点可以看成是索引部分，结点中仅含其子树（根结点）中的最大（或最小）关键字。
   通常在B+树上有两个头指针，一个指向根结点，一个指向关键字最小的叶子结点。

• 特点
  其定义基本与B-树同，除了：

1. 非叶子结点的子树指针与关键字个数相同(据July，有争议)；
2. 非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；
3. 所有关键字都在叶子结点出现；

一般在数据库系统或文件系统中使用的B+Tree结构都在经典B+Tree的基础上进行了优化，增加了顺序访问指针，如下图：

在B+Tree的每个叶子节点增加一个指向相邻叶子节点的指针(链指针)，就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能，例如图4中如果要查询key为从18到49的所有数据记录，当找到18后，只需顺着节点和指针顺序遍历就可以一次性访问到所有数据节点，极大提到了区间查询效率。

• 使用

B+树的基本操作：
查找操作
对B+树可以进行两种查找运算：
　　a.从最小关键字起顺序查找；
　　b.从根结点开始，进行随机查找。
　　在查找时，若非终端结点上的剧组机等于给定值，并不终止，而是继续向下直到叶子结点。因此，在B+树中，不管查找成功与否，每次查找都是走了一条从根到叶子结点的路径。其余同B-树的查找类似。
插入操作
B+树的插入与B树的插入过程类似。不同的是B+树在叶结点上进行，如果叶结点中的关键码个数超过m，就必须分裂成关键码数目大致相同的两个结点，并保证上层结点中有这两个结点的最大关键码。(算法见百度百科)
删除操作
B+树的删除也仅在叶子结点进行，当叶子结点中的最大关键字被删除时，其在非终端结点中的值可以作为一个“分界关键字”存在。若因删除而使结点中关键字的个数少于m/2 （m/2结果取上界，如5/2结果为3）时，其和兄弟结点的合并过程亦和B-树类似。

如M=3:

1. 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
2. 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
3. 更适合文件索引系统（见FAQ）；

## B-树

B-树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针：
M=3:

与B+-树区别：

• B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据
  复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；
• B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分
  数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

红黑树（不追求“完全平衡”）

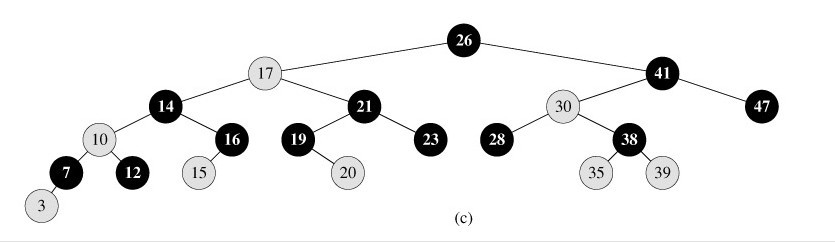
1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点，即空结点（NIL）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。

这些约束的好处是：保持了树的相对平衡，同时又比AVL的插入删除操作的复杂性要低许多。

• 由于它的设计，任何不平衡都会在三次旋转之内解决,AVL树有最多O(logN)次旋转。
• 如果插入一个node引起了树的不平衡，AVL和RB-Tree都是最多只需要2次旋转操作，即两者都是O(1)；但是在删除node引起树的不平衡时，最坏情况下，AVL需要维护从被删node到root这条路径上所有node的平衡性，因此需要旋转的量级O(logN)，而RB-Tree最多只需3次旋转，只需要O(1)的复杂度。
• 其次，AVL的结构相较RB-Tree来说更为平衡，在插入和删除node更容易引起Tree的unbalance，因此在大量数据需要插入或者删除时，AVL需要rebalance的频率会更高。因此，RB-Tree在需要大量插入和删除node的场景下，效率更高。自然，由于AVL高度平衡，因此AVL的search效率更高。
• map的实现只是折衷了两者在search、insert以及delete下的效率。总体来说，RB-tree的统计性能是高于AVL的。

http://www.importnew.com/21818.html

为什么需要红黑树？

map,set底层都提供了排序功能，且查找速度快。红黑树实际上是AVL的一种变形，但是其比AVL(平衡二叉搜索树)具有更高的插入效率，当然查找效率会平衡二叉树稍微低一点点，毕竟平衡二叉树太完美了。但是这种查找效率的损失是非常值得的。它的操作有着良好的最坏情况运行时间，并且在实践中是高效的: 它可以在O(logn)时间内做查找，插入和删除，这里的n是树中元素的数目。

排序

堆排序

输入无序序列 { 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 } ，如下所示，先建最大堆，建立最大堆的过程是先将原序列按照完全二叉树的顺序进行排列，然后从N/2个节点（向下取整）开始进行交换。
建完堆之后，再利用堆调整过程不断取堆顶，最终获得排序后结果。

几种常见的数据结构的操作性能对比

关于树的FAQ

• 红黑树用于内存搜索，磁盘搜索用的多是多路树？
  因为磁盘读取效率是很慢的，读取次数是基于树高度，所以像数据库中的B/B+索引都是多路树，每一个block中存放多个子节点信息，减少磁盘读取次数。
• 为什么说B+-tree比B树更适合实际应用中操作系统的文件索引和数据库索引？

1. B+-tree的磁盘读写代价更低
   B+-tree的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
   举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快（28+28）。而B+树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候（查找是基于节点信息），B 树就比B+ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。
2. B+-tree的查询效率更加稳定（查询时间的均衡）
   由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

读者点评：

本文评论下第149楼，fanyy1991针对上文所说的两点，道：个人觉得这两个原因都不是主要原因。数据库索引采用B+树的主要原因是（上述从检索的角度，这里从遍历的角度）：
B-树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题，B+树应运而生。B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作（或者说效率太低）。

• 不同的引擎对于索引有不同的支持：Innodb和MyISAM默认的索引是Btree索引（之后版本B+树）；而Memory默认的索引是Hash索引（哈希值可能重复，所以检索效率未必就高）。